
| Palaeos |  |
Mollusca |
| Metazoa | The Shell |
| Page Back: Mollusca | Unit Up: Metazoa | Unit Home | Mollusca Glossary | Page Next: Phylogeny |
| Unit Back: Annelida |
Clade Down: Aculifera Conchifera |
Mollusca Dendrogram | Mollusca References | Unit Next: Platyzoa |
|
Abbreviated Dendrogram
SPIRALIA |--BRACHIOPODA `--+--ANNELIDA | `--MOLLUSCA |--Aculifera | |==Turrilepadida | `-- Polyplacophora `--Conchifera |==Tryblidiida (Monoplacophora) | `--Cephalopoda `==Helcionelloida |==Rostroconchia | `-- Scaphopoda |--Bivalvia `--Gastropoda |
Contents
Overview |
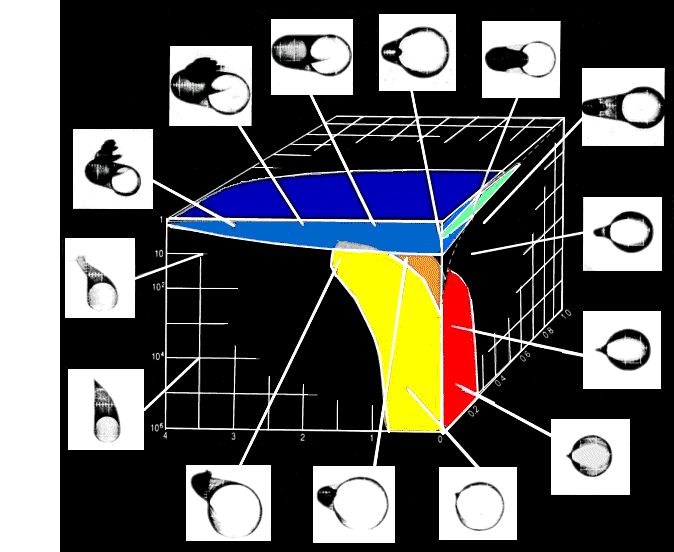
image from Equiangular Spiral Mollusca
The work of ![]() D'Arcy Wentworth Thompson - especially his opus On Growth and Form, was seminal in
understanding the elegant mathematical basis of the forms found in nature, such as
mollusk shells, plant growth, and so on. Of later studies regarding the theoretical morphology of the coiled shell, the work of David Raup
(1962, 1966) is the best-known. Raup used a computer-based graphical method to produce a range of hypothetical coiled shapes and was then
able to see how many of these possible types had in fact been adopted in nature. [Clarkson, 1979 p.141].
D'Arcy Wentworth Thompson - especially his opus On Growth and Form, was seminal in
understanding the elegant mathematical basis of the forms found in nature, such as
mollusk shells, plant growth, and so on. Of later studies regarding the theoretical morphology of the coiled shell, the work of David Raup
(1962, 1966) is the best-known. Raup used a computer-based graphical method to produce a range of hypothetical coiled shapes and was then
able to see how many of these possible types had in fact been adopted in nature. [Clarkson, 1979 p.141].
Dr Raup was able to generate a large number of ideal shapes using only four parameters, three of which are shown here:
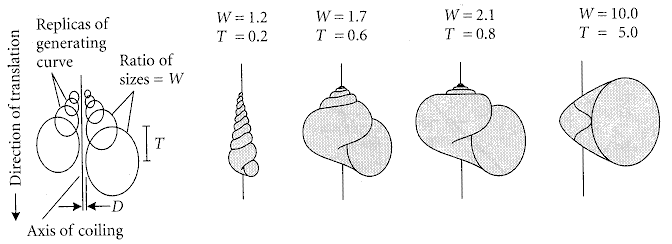
"A simple model of variation in the rate of growth in several dimensions accounts for variation in the form of gastropod shells. The model specifies the shape of the aperture, or generating curve, the axis of coiling, the size ratio (W) of successive generating curves, the distance (D) of the generating curve from the axis, and the proportion (T) of the height of one generating curve that is covered by the successive gyres."
Taking the example of a helically coiled gastropod, and assuming that its shell is no more than a long hollow cone growing at the aperture end and coiling about a vertical axis as it grows, these parameters are:
Some transitional forms are shown in the following diagram, from Futuyma 1997, after Raup 1962
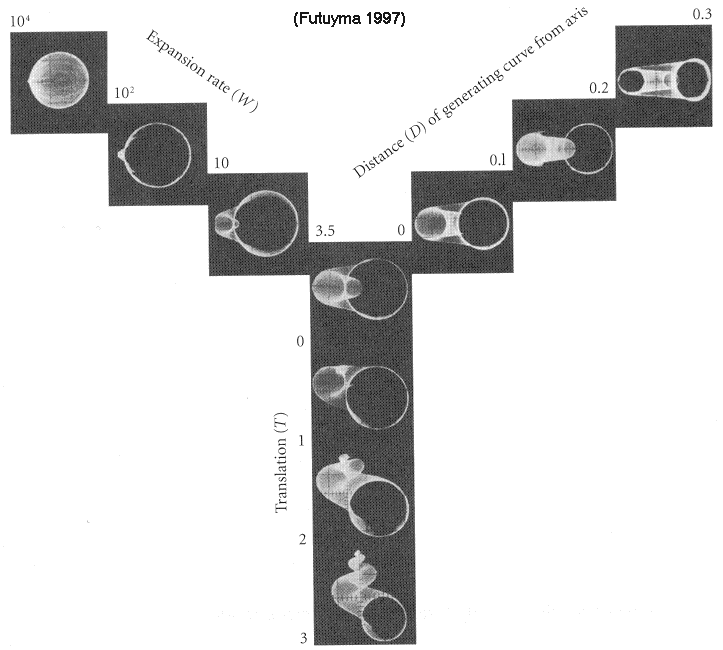
Originally, the shell shapes were projected onto an oscilloscope screen. Four decades later, anyone can access experiment by means of a simple ![]() java applet available on the Web
java applet available on the Web
One can easily see how some molluscs, and indeed some spiral forms in nature (since these principles can be widely applied) developed shells where certain parameters have a high value, and others a low value. This is because each form evolved to different functional ends. Thus gastropods are usually helically coiled and tend to have a low W but T is very variable and may be anywhere from fairly low (giving squat broad shells) to extremely high, giving very tall high-spired shells. A few planispiral gastropods have T of value 0 (giving a shell equivalent in shape to coiled cephalopods, but lacking septa), and in one extinct lineage, the Euomphalids, T that is positive. In contrast, paragastropods have T that is positive in value, and may be very low to moderate. In bivalves T is always low and W is always very high, giving shells with a wide open curve and very rapidly expanding apertures. In brachiopods W is also high but T always equals O. Cephalopods are with only a few exceptions T=0 (planispiral), but unlike Brachiopods W is almost always very low (although some endocerids and other brevicones had short broad shells, but even here W is much lower even than in limpet gastropods). The following diagram shows some variations in form with only two parameters. The vertical axis here = W, the horizontal axis = D.
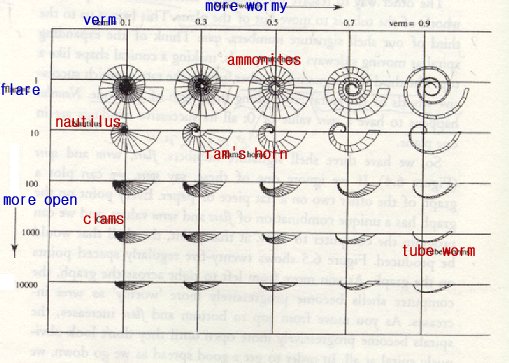
Dr Raup showed that coiled molluscs occupied only a small part of available geometric morphospace. Of all the possible shell shapes he was able to generate only relatively few have been found biologically useful, and these shapes were thus been adopted repeatedly within certain groups. Other types have not been able to be put to useful functional purposes and so are rarely, if ever, found in any living or fossil group. [Clarkson, 1979 p.142]. Choice of particular form can be the result of a complex process. The distribution of ammonoid shells does not appear to represent the optimization of any single functional factor, but rather is a geometric region which minimizes several problems. [Saunders et al 2002].
| Links |
 Computer generated snail shells - This applet lets you create images of shells using Raup's mathematical model of shell form.
Computer generated snail shells - This applet lets you create images of shells using Raup's mathematical model of shell form.
![]() Raup Model - more images according to Raup 1962
Raup Model - more images according to Raup 1962
![]() Computational Paleontology - includes
modeling ammonoid ribs, ammonite sutures, Graptolite growth, Logarithmic spirals (e.g.
mollusk shells), Ammonoid septa, and Coral septa
Computational Paleontology - includes
modeling ammonoid ribs, ammonite sutures, Graptolite growth, Logarithmic spirals (e.g.
mollusk shells), Ammonoid septa, and Coral septa
| Page Back: Mollusca | Page Top | Unit Home | Page Next: Phylogeny |